
Ο Ευκλείδης και η Γέννηση της Γεωμετρίας
Δεν είναι μυστικό ότι πολλοί από εμάς δεν αγαπάμε πολύ τα μαθηματικά και τη γεωμετρία και ότι συχνά είναι πολύ περίπλοκα. Αλλά ακόμα κι έτσι, μπορεί να είναι αρκετά εντυπωσιακό να κοιτάξουμε πίσω στην ιστορία και να ανακαλύψουμε τους αρχαίους στοχαστές που ήταν πολύ μπροστά από την εποχή τους και έχουν καταλήξει σε περίπλοκα θεωρήματα, καινοτομίες και ανακαλύψεις στον τομέα των μαθηματικών. Ένας τέτοιος πρωτοπόρος της επιστημονικής σκέψης είναι ο Ευκλείδης, ο Αρχαίος Έλληνας μαθηματικός που άκμασε γύρω στο 300 π.Χ., και θεωρείται ο πατέρας της γεωμετρίας.
Γεννημένος στην Αλεξάνδρεια της Αιγύπτου , η ζωή και η κληρονομιά του έχουν γίνει αντικείμενο γοητείας και σεβασμού για τους μελετητές ανά τους αιώνες. Επιπλέον, το πιο σημαντικό έργο του, «Στοιχεία», όχι μόνο έθεσε τα θεμέλια για τη μελέτη της γεωμετρίας αλλά επίσης επηρέασε βαθιά την ανάπτυξη των μαθηματικών στο σύνολό της. Ας μάθουμε περισσότερα για αυτόν τον άνθρωπο που ήταν μπροστά από την εποχή του.
Ο Ευκλείδης έθεσε τα θεμέλια της σύγχρονης γεωμετρίας
Η πρώιμη ζωή και η εκπαίδευση του Ευκλείδη δεν είναι πολύ καλά τεκμηριωμένα, αφήνοντας τους ιστορικούς να συνδυάσουν θραύσματα αποδεικτικών στοιχείων και εικασίες για να σχηματίσουν ένα πορτρέτο του ανθρώπου πίσω από τον μαθηματικό μύθο. Ενώ οι ακριβείς λεπτομέρειες μας διαφεύγουν, οι εικασίες και τα συμπεράσματα παρέχουν δελεαστικές ματιές στα χρόνια της μόρφωσής του. Οι σύγχρονοι ιστορικοί συμφωνούν γενικά ότι ο Ευκλείδης έλαβε την εκπαίδευσή του στην Ακαδημία της Αθήνας, το πνευματικό επίκεντρο του αρχαίου κόσμου. Σε αυτή τη ζωντανή πόλη άκμασαν οι φιλοσοφικές και μαθηματικές ιδέες προσωπικοτήτων όπως ο Πλάτωνας και οι οπαδοί του. Ορισμένες μαρτυρίες υποδηλώνουν ότι ο Ευκλείδης μπορεί να ήταν μαθητής της Ακαδημίας του Πλάτωνα ή να σπούδασε κάτω από μαθητές του Πλάτωνα, εμποτίζοντας τα φιλοσοφικά ερείσματα που αργότερα θα ενίσχυαν τις μαθηματικές του προσπάθειες.
Μια άλλη συναρπαστική πιθανότητα είναι ότι η εκπαίδευση του Ευκλείδη επηρεάστηκε από την Πυθαγόρεια σχολή σκέψης. Οι Πυθαγόρειοι, γνωστοί για τη γοητεία τους με τη γεωμετρία και τον μαθηματικό μυστικισμό, άσκησαν βαθιά επιρροή στο πνευματικό περιβάλλον της αρχαίας Ελλάδας. Η έμφαση του Ευκλείδη στη γεωμετρική αφαίρεση και την αυστηρή απόδειξη μπορεί να αντανακλά την πυθαγόρεια τάση για μαθηματική καθαρότητα και λογική εξαγωγή. Ανεξάρτητα από τις ιδιαιτερότητες της επίσημης εκπαίδευσής του, είναι προφανές ότι ο Ευκλείδης αναδύθηκε από αυτό το χωνευτήριο της πνευματικής μάθησης με μια βαθιά εκτίμηση για τη δύναμη του απαγωγικού συλλογισμού και της λογικής επιχειρηματολογίας. Η μαθηματική του ικανότητα και η παιδαγωγική του οξυδέρκεια θα βρουν αργότερα έκφραση στο magnum opus του, “Elements”, μια απόδειξη της δεξιοτεχνίας του στη γεωμετρία και της ικανότητάς του να αποστάζει περίπλοκες μαθηματικές έννοιες σε κομψές, λογικές αποδείξεις.
Ελλείψει συγκεκριμένων βιογραφικών λεπτομερειών, αφήνουμε να κάνουμε εικασίες σχετικά με τις επιρροές που διαμόρφωσαν την πρώιμη ζωή και την εκπαίδευση του Ευκλείδη. Ήταν φυσικό ταλέντο; Ή εμπνεύστηκε από τους μεγάλους που ήρθαν πριν από αυτόν; Όποια και αν είναι η περίπτωση, αυτό που παραμένει πέρα από κάθε αμφιβολία είναι η διαρκής κληρονομιά της μαθηματικής του ιδιοφυΐας, η οποία συνεχίζει να προκαλεί δέος και θαυμασμό σε μαθηματικούς και μελετητές μέχρι σήμερα. Το ταξίδι του Ευκλείδη από την αφάνεια των αρχαίων χρόνων στις αγιασμένες αίθουσες της μαθηματικής αθανασίας στη σύγχρονη, επιστημονική εποχή χρησιμεύει ως απόδειξη της δύναμης της ανθρώπινης διάνοιας και της διαχρονικής αναζήτησης για γνώση και κατανόηση.

Πίνακας του 1650 του Ευκλείδη του μαθηματικού.
Ο Ευκλείδης και η Γέννηση της Γεωμετρίας
Η γέννηση της γεωμετρίας αντιπροσωπεύει μια κομβική στιγμή στην εξέλιξη του ανθρώπινου πολιτισμού, σηματοδοτώντας την αυγή της συστηματικής έρευνας για τις ιδιότητες του χώρου, του σχήματος και της μορφής. Ενώ οι απαρχές της γεωμετρίας μπορούν να αναχθούν στις πρακτικές ανάγκες των αρχαίων κοινωνιών, όπως η γεωγραφία και ο αρχιτεκτονικός σχεδιασμός, η επισημοποίησή της ως μαθηματικός κλάδος οφείλεται σε μεγάλο βαθμό στις πνευματικές προσπάθειες αρχαίων Ελλήνων μελετητών όπως ο Θαλής, ο Πυθαγόρας και, κυρίως , Ευκλείδης. Η γεωμετρία προέκυψε οργανικά από την παρατήρηση και το χειρισμό φυσικών αντικειμένων στον φυσικό κόσμο. Οι αρχαίοι πολιτισμοί, όπως οι Αιγύπτιοι και οι Βαβυλώνιοι, ανέπτυξαν στοιχειώδεις γεωμετρικές έννοιες για να διευκολύνουν εργασίες όπως η μέτρηση των ορίων της γης, η κατασκευή κτιρίων και η πρόβλεψη ουράνιων γεγονότων. Αυτές οι πρώιμες γεωμετρικές αρχές έθεσαν τις βάσεις για την πιο αφηρημένη και συστηματική προσέγγιση της γεωμετρίας που θα εμφανιστεί αργότερα στην αρχαία Ελλάδα.

Ένας φωτισμός από ένα χειρόγραφο που βασίζεται στη μετάφραση του Adelard of Bath των Elements, 1309–1316. Το Adelard’s είναι η παλαιότερη σωζόμενη μετάφραση των Στοιχείων στα Λατινικά. ( Δημόσιος τομέας )
Η ελληνική έννοια των “γεωμετριών”, που σημαίνει “γήινη μέτρηση” ή “τοποθέτηση γης”, αντανακλά την πρακτική προέλευση της γεωμετρίας στη μέτρηση και τη διαίρεση της γης. Ωστόσο, ήταν οι Έλληνες φιλόσοφοι και μαθηματικοί που προσπάθησαν να ανυψώσουν τη γεωμετρία από μια χρηστική τέχνη σε μια αυστηρή πνευματική αναζήτηση. Ο Θαλής της Μιλήτου , που συχνά θεωρείται ο πρώτος μαθηματικός, πιστώνεται ότι εισήγαγε τον απαγωγικό συλλογισμό και τη μαθηματική αφαίρεση στη γεωμετρία. Το θεώρημά του σχετικά με τις ιδιότητες των τριγώνων που σχηματίζονται από τεμνόμενες ευθείες έθεσε τα θεμέλια για την επακόλουθη γεωμετρική έρευνα. Οι Πυθαγόρειοι, οπαδοί του φιλόσοφου Πυθαγόρα , προώθησαν περαιτέρω τη μελέτη της γεωμετρίας, εμποτίζοντας την με μια αίσθηση μαθηματικού μυστικισμού και φιλοσοφικής σημασίας. Το Πυθαγόρειο θεώρημα , το οποίο συσχετίζει τα μήκη των πλευρών ενός ορθογωνίου τριγώνου, παραμένει ένα από τα πιο διάσημα αποτελέσματα στη γεωμετρία και μια απόδειξη της δύναμης του μαθηματικού συλλογισμού.
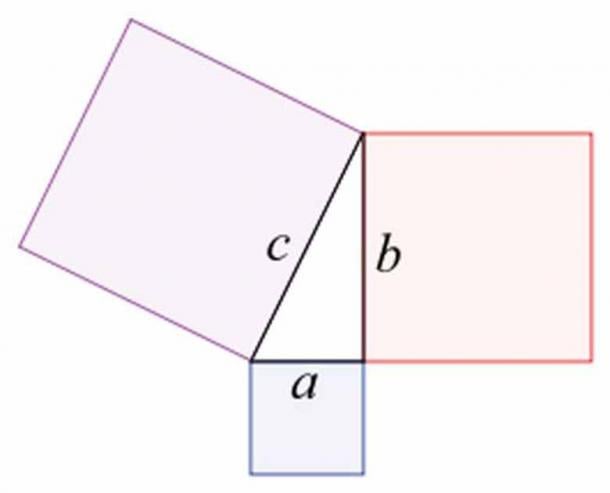
Απεικόνιση του Πυθαγόρειου θεωρήματος. ( CC BY SA 3.0 )
Ωστόσο, ο Ευκλείδης ήταν αυτός που κωδικοποίησε και συστηματοποίησε τις ανόμοιες γεωμετρικές αρχές των προκατόχων του σε ένα ολοκληρωμένο πλαίσιο γνωστό ως «Ευκλείδεια γεωμετρία». Το μεγάλο έργο του, “Στοιχεία”, χρησίμευσε ως το οριστικό εγχειρίδιο γεωμετρίας για περισσότερες από δύο χιλιετίες, παρέχοντας μια αυστηρή βάση για τη μελέτη γεωμετρικών αρχών, θεωρημάτων και αποδείξεων. Η αξιωματική προσέγγιση του Ευκλείδη στη γεωμετρία, η οποία στηρίχθηκε σε ένα μικρό σύνολο αυτονόητων αληθειών γνωστών ως αξιώματα, έθεσε τις βάσεις για την απαγωγική μέθοδο που θα γινόταν το σήμα κατατεθέν του μαθηματικού συλλογισμού. Οργανώνοντας τις γεωμετρικές έννοιες σε μια λογική και ιεραρχική δομή, ο Ευκλείδης καθιέρωσε τη γεωμετρία ως μια πειθαρχία που βασίζεται σε αυστηρή απόδειξη και λογική επιχειρηματολογία. Η γέννηση της γεωμετρίας αντιπροσωπεύει έναν θρίαμβο της ανθρώπινης διανόησης και περιέργειας, μετατρέποντας τις πρακτικές ανησυχίες των αρχαίων πολιτισμών σε μια διαχρονική πνευματική αναζήτηση.
Ένας άνθρωπος που χάραξε το όνομά του στην ιστορία
Το θεμελιώδες αριστούργημα του Ευκλείδη είναι το βιβλίο «Στοιχεία», μια πραγματεία δεκατριών βιβλίων και το magnum έργο του. Ήταν ένα μνημειώδες επίτευγμα στην ιστορία των μαθηματικών, που χρησίμευσε ως το βασικό εγχειρίδιο για τη γεωμετρία για περισσότερες από δύο χιλιετίες. Η πραγματεία θέτει σχολαστικά τα θεμέλια της Ευκλείδειας γεωμετρίας και θέτει τα πρότυπα για τη μαθηματική έκθεση, τη λογική συλλογιστική και την αυστηρή απόδειξη. Τα δεκατρία βιβλία είναι τα εξής:
- Βιβλίο Ι – Βασικές Γεωμετρία Επίπεδου:
Αυτό το βιβλίο εκθέτει τις θεμελιώδεις έννοιες της γεωμετρίας, συμπεριλαμβανομένων των σημείων, των γραμμών, των γωνιών και των επιπέδων. Εισάγει τα διάσημα πέντε αξιώματα ή αξιώματα του Ευκλείδη, τα οποία χρησιμεύουν ως βάση για όλους τους επόμενους γεωμετρικούς συλλογισμούς. - Βιβλίο ΙΙ – Γεωμετρική Άλγεβρα:
Το βιβλίο ΙΙ διερευνά τις ιδιότητες των γεωμετρικών σχημάτων όπως τα τρίγωνα, τα παραλληλόγραμμα και οι κύκλοι. Εισάγει έννοιες όπως η αναλογικότητα και η ομοιότητα, θέτοντας τις βάσεις για πιο προηγμένο γεωμετρικό συλλογισμό. - Βιβλίο III – Ιδιότητες Κύκλων:
Αυτό το βιβλίο είναι αφιερωμένο στη μελέτη των κύκλων, συμπεριλαμβανομένων των ιδιοτήτων των χορδών, των εφαπτομένων και των εγγεγραμμένων γωνιών. - Βιβλίο IV – Κανονικό Πολύεδρο:
Το βιβλίο IV εστιάζει στις ιδιότητες των κανονικών στερεών, όπως το τετράεδρο, ο κύβος και το δωδεκάεδρο. Εισάγει την έννοια των πλατωνικών στερεών και διερευνά τις γεωμετρικές τους ιδιότητες. - Βιβλίο V – Θεωρία των αναλογιών:
Το βιβλίο V εμβαθύνει στη θεωρία των αναλογιών και των αναλογιών, συμπεριλαμβανομένων των ιδιοτήτων των γεωμετρικών μέσων και των θεωρημάτων που σχετίζονται με την αναλογικότητα. - Βιβλίο VI – Παρόμοιες φιγούρες:
Αυτό το βιβλίο διερευνά τις ιδιότητες παρόμοιων σχημάτων και τις σχέσεις μεταξύ των αντίστοιχων πλευρών και γωνιών. - Βιβλίο VII – Θεωρία Αριθμών:
Το βιβλίο VII εισάγει τη θεωρία των αριθμών, συμπεριλαμβανομένων των ιδιοτήτων των πρώτων, της διαιρετότητας και του αλγόριθμου για την εύρεση του μεγαλύτερου κοινού διαιρέτη. - Βιβλίο VIII – Αριθμητικές και Γεωμετρικές Προόδους:
Το βιβλίο VIII εξετάζει αριθμητικές και γεωμετρικές προόδους, συμπεριλαμβανομένων των ιδιοτήτων των αθροισμάτων όρων και των θεωρημάτων που σχετίζονται με αυτές τις ακολουθίες. - Βιβλίο IX – Θεωρία Αριθμών Συνέχεια:
Αυτό το βιβλίο συνεχίζει την εξερεύνηση της θεωρίας αριθμών, συμπεριλαμβανομένων των ιδιοτήτων των τέλειων αριθμών, της παραγοντοποίησης πρώτων και του Ευκλείδειου αλγόριθμου. - Βιβλίο Χ – Παράλογοι Αριθμοί και Γεωμετρική Άλγεβρα:
Το βιβλίο Χ εισάγει την έννοια των παράλογων αριθμών και διερευνά τη σχέση τους με γεωμετρικά μεγέθη όπως μήκη και εμβαδά. - Βιβλίο XI – Στερεά Γεωμετρία:
Το βιβλίο XI εστιάζει στη στερεά γεωμετρία, συμπεριλαμβανομένων των ιδιοτήτων των κώνων, των κυλίνδρων και των σφαιρών. Διερευνά επίσης τη σχέση μεταξύ των όγκων και των επιφανειών αυτών των στερεών. - Βιβλίο XII – Το Δωδεκάεδρο και οι ιδιότητές του:
Αυτό το βιβλίο είναι αφιερωμένο στη μελέτη του δωδεκάεδρου, ενός από τα πέντε πλατωνικά στερεά, και των γεωμετρικών του ιδιοτήτων. - Βιβλίο XIII – Μέθοδος του Αρχιμήδη:
Το τελευταίο βιβλίο των «Στοιχείων» είναι μια συλλογή αποτελεσμάτων που αποδίδονται στον μαθηματικό Αρχιμήδη , συμπεριλαμβανομένης της μέτρησης των κύκλων και του υπολογισμού των όγκων των διαφόρων στερεών.
Τα «Στοιχεία» του Ευκλείδη είναι διάσημα για τη συστηματική οργάνωση, τη λογική αυστηρότητα και την έμφαση στον απαγωγικό συλλογισμό. Κάθε πρόταση δηλώνεται με σαφήνεια και ακρίβεια, ακολουθούμενη από μια αυστηρή απόδειξη που βασίζεται σε προηγουμένως καθορισμένα αποτελέσματα. Η αξιωματική μέθοδος του Ευκλείδη, η οποία ξεκινά με ένα μικρό σύνολο αυτονόητων αληθειών και αντλεί περαιτέρω αποτελέσματα μέσω λογικής εξαγωγής, θέτει τα πρότυπα για τη μαθηματική έκθεση. Η επιρροή του magnum opus του Ευκλείδη εκτείνεται πολύ πέρα από τη σφαίρα της γεωμετρίας, διαμορφώνοντας την πορεία της μαθηματικής έρευνας για αιώνες. Η έμφαση που δίνει στον λογικό συλλογισμό, την αυστηρή απόδειξη και τη συστηματική οργάνωση χρησιμεύει ως μοντέλο για μαθηματική έκθεση σε πεδία που κυμαίνονται από την άλγεβρα και τη θεωρία αριθμών έως τον λογισμό και όχι μόνο.

Ο Ευκλείδης θεωρείται ο πατέρας της γεωμετρίας. Τα στοιχεία, ένα απόσπασμα των οποίων παρουσιάζεται εδώ, είναι ένα από τα πιο σημαντικά έργα στην ιστορία των μαθηματικών. ( Δημόσιος τομέας )
Αιώνες μπροστά από την εποχή Του
Οι συνεισφορές του Ευκλείδη στα μαθηματικά εκτείνονται πολύ πέρα από τη σφαίρα της γεωμετρίας, καλύπτοντας ένα ευρύ φάσμα μαθηματικών κλάδων και θέτοντας τις βάσεις για πολλές θεμελιώδεις έννοιες και μεθόδους που συνεχίζουν να διαμορφώνουν το πεδίο μέχρι σήμερα. Ενώ είναι πιο γνωστός για το έργο του στη γεωμετρία, ιδιαίτερα για το μεγάλο έργο του, η επιρροή του Ευκλείδη ξεπερνά αυτόν τον μοναδικό κλάδο, αγγίζοντας τη θεωρία των αριθμών, την άλγεβρα και τη μαθηματική λογική. Για παράδειγμα, τα «Στοιχεία» του Ευκλείδη εισήγαγαν την αξιωματική μέθοδο στη μαθηματική έρευνα, θέτοντας τα θεμέλια για την απαγωγική προσέγγιση που θα γινόταν το χαρακτηριστικό γνώρισμα του μαθηματικού συλλογισμού. Ξεκινώντας με ένα σύνολο αξιωμάτων, ή αυτονόητων αληθειών, και αντλώντας περαιτέρω αποτελέσματα μέσω λογικής εξαγωγής, ο Ευκλείδης δημιούργησε ένα αυστηρό πλαίσιο για μαθηματική απόδειξη που συνεχίζει να επηρεάζει το πεδίο μέχρι σήμερα. Η αξιωματική μέθοδος παρέχει μια σταθερή βάση για την οικοδόμηση μαθηματικών θεωριών και διασφαλίζει τη σαφήνεια και την ακρίβεια των μαθηματικών επιχειρημάτων.

Μια σελίδα με περιθώρια από την πρώτη έντυπη έκδοση των Euclid’s Elements, που τυπώθηκε από τον Erhard Ratdolt το 1482. (Erhard Ratdolt/ CC BY-SA 4.0 )
Η επιρροή του μπορεί επίσης να φανεί στην ανάπτυξη αλγεβρικών μεθόδων. Η εργασία του για τις αναλογίες και τις αναλογίες έθεσε τις βάσεις για την αλγεβρική συλλογιστική, ιδιαίτερα στο πλαίσιο της επίλυσης εξισώσεων και του χειρισμού αλγεβρικών εκφράσεων. Η Ευκλείδεια γεωμετρία παρείχε μια γεωμετρική ερμηνεία για τις αλγεβρικές έννοιες και η έμφαση του στη λογική συλλογιστική και την αυστηρή απόδειξη έθεσε το έδαφος για την ανάπτυξη σύγχρονων αλγεβρικών δομών και τεχνικών.
Επιπλέον, συνέβαλε επίσης σημαντικά στη θεωρία αριθμών, ιδιαίτερα στη θεωρία των πρώτων. Το βιβλίο VII των “Στοιχείων” είναι αφιερωμένο στη μελέτη της θεωρίας αριθμών, συμπεριλαμβανομένων των ιδιοτήτων των πρώτων, της διαιρετότητας και του αλγόριθμου για την εύρεση του μεγαλύτερου κοινού διαιρέτη. Ο αλγόριθμος του Ευκλείδη για την εύρεση του μεγαλύτερου κοινού διαιρέτη δύο αριθμών παραμένει θεμελιώδες εργαλείο στη θεωρία αριθμών και έχει εφαρμογές σε τομείς όπως η κρυπτογραφία και η επιστήμη των υπολογιστών.
Αγαπημένο από φοιτητές σε όλο τον κόσμο
Τελικά, είναι απίστευτο πώς οι συνεισφορές ενός ανθρώπου στα μαθηματικά είχαν βαθύ και διαρκή αντίκτυπο στο πεδίο, διαμορφώνοντας την πορεία της μαθηματικής έρευνας για αιώνες. Η έμφαση του Ευκλείδη στον λογικό συλλογισμό, την αυστηρή απόδειξη και τη συστηματική οργάνωση έθεσε το πρότυπο για τη μαθηματική έκθεση και έθεσε τις βάσεις για πολλές θεμελιώδεις έννοιες και μεθόδους στα μαθηματικά. Από την αξιωματική του μέθοδο μέχρι τις γνώσεις του για τη γεωμετρία, τη θεωρία αριθμών και την άλγεβρα, η κληρονομιά του Ευκλείδη συνεχίζει να εμπνέει και να ενημερώνει μαθηματικούς και μελετητές μέχρι σήμερα, υπενθυμίζοντάς μας τη διαχρονική ομορφιά και κομψότητα της μαθηματικής αλήθειας.
Επάνω εικόνα: Αριστερά, Ζωγραφική του Ευκλείδη. Δεξιά, Μια σελίδα πρώτη έντυπη έκδοση των Euclid’s Elements. Πηγή: Fondazione Cariplo/ CC BY-SA 3.0 ; Erhard Ratdolt / CC BY-SA 4.0
Του Aleksa Vučković
βιβλιογραφικές αναφορές
Artmann, B. 1999. Euclid: The Creation of Mathematics. Springer Publishing.
Ball, WWR 1960. A Short Account of the History of Mathematics (4th ed.). Εκδόσεις Ντόβερ.
Heath, T. 1908. The Thirteen Books of Euclid’s Elements. Τομ. 1. Εκδόσεις Ντόβερ.




